El límite y el valor de la función coinciden: Se dice que una función es continua en un intervalo si es continua en todos sus puntos. Si f (x1)= y1, la continuidad en x1 se expresa así: parafraseando, cuando x se aproxima a x1, f (x) se aproxima a y1. Por definición de los límites, esto significa que para todo intervalo abierto J.. Cuando una función es continua dentro de su dominio, es una función continua. ¡Formalidad! Podemos definir continuidad usando Límites (ayuda leer esa página primero):. Una función f es continua cuando, para cada valor c en su dominio:. f(c) está definida, y. limx→c f(x) = f(c) “el límite de f(x) cuando x se acerca a c es igual a f(c)”
Funció continua

Caracteristicas De Las Funciones Lineales Trilosa

Continuidad de funciones Funciones Continuas y discontinuas Explicación completa con

(PDF) 6. Funciones continuas Jessica Cuevas Academia.edu

2. CONTINUIDAD Y DERIVABILIDAD. Cómo saber si una función es continua. Parte II. YouTube

Funciones continuas y discontinuas (Tipos de Discontinuidad) YouTube
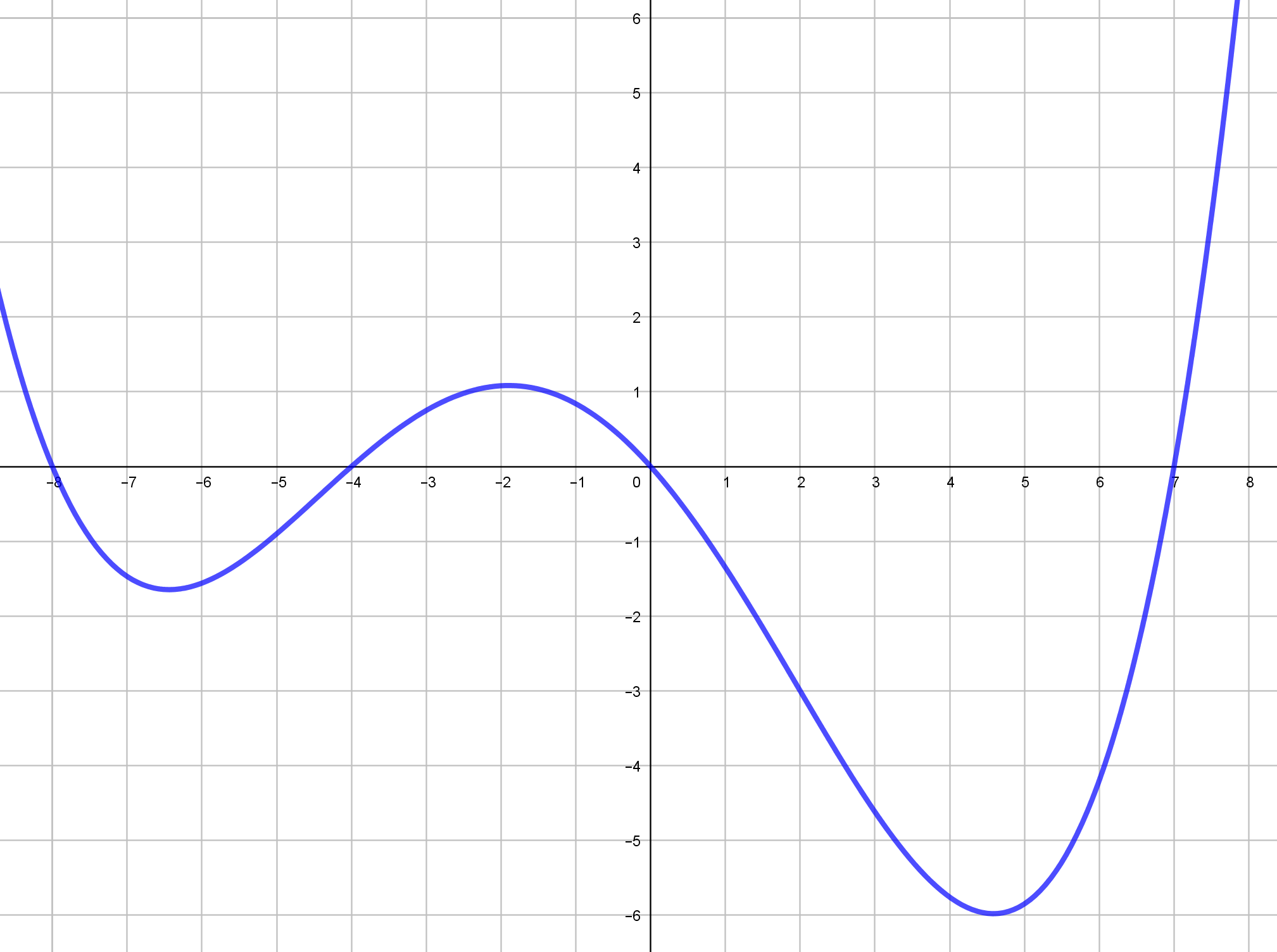
Continuidad Funciones más allá del libro de texto

Características de una función YouTube

Límites y continuidad Propiedades de las funciones continuas YouTube
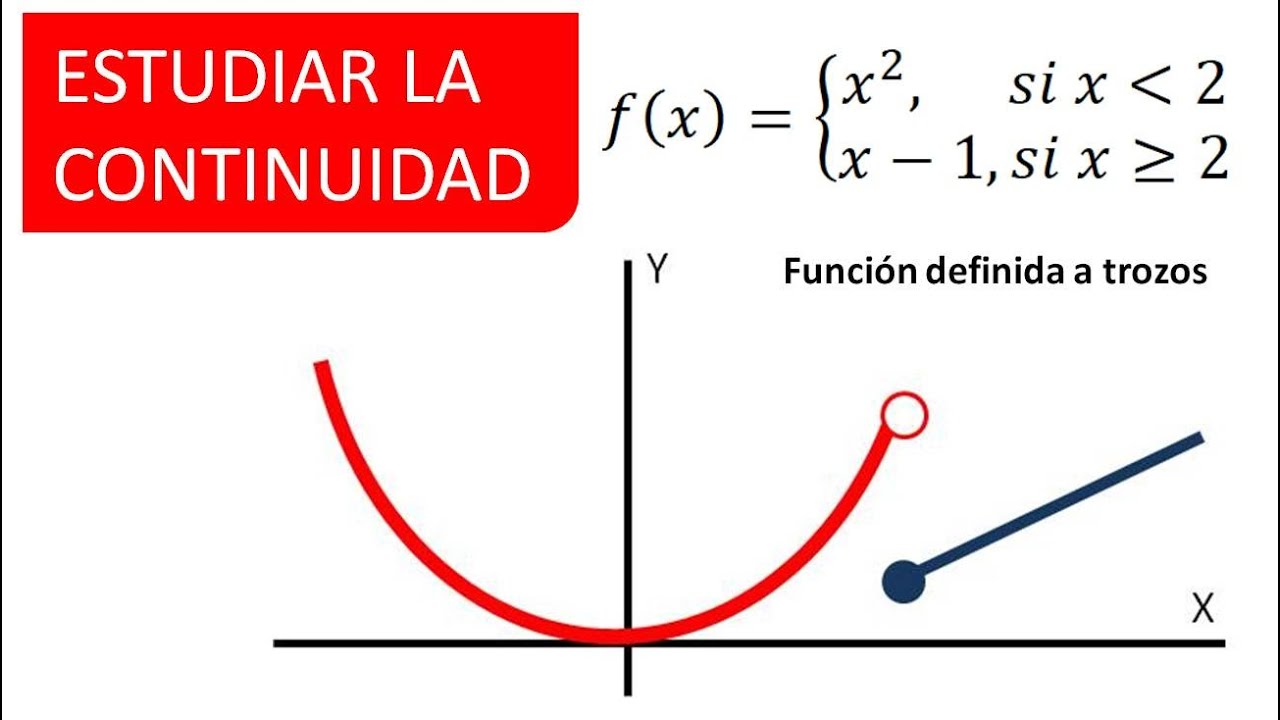
ESTUDIO DE LA CONTINUIDAD. FUNCIÓN DEFINIDA A TROZOS YouTube
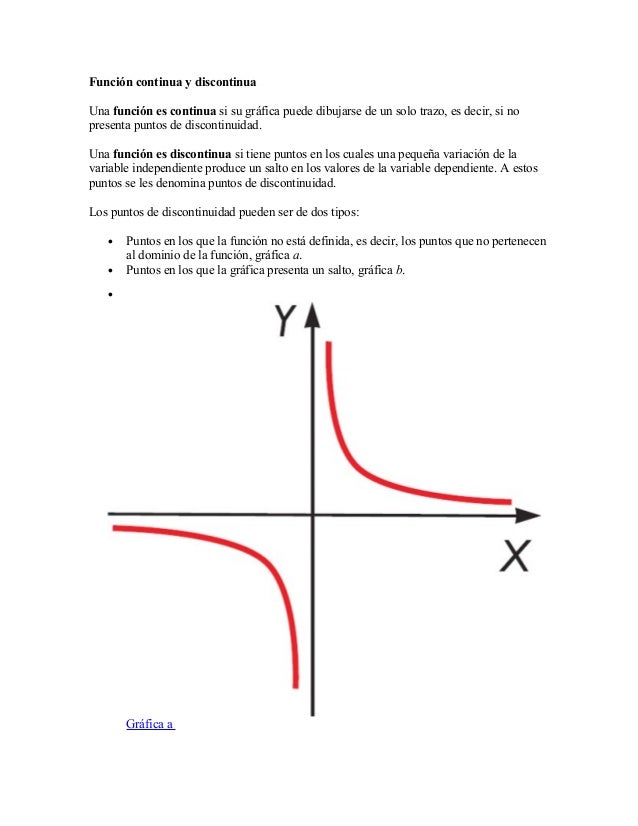
Aprende a graficar funciones continuas y discontinuas paso a paso

Función contínua Definición Condiciones y ejercicios YouTube

Funciones continuas

Propiedades de las funciones continuas YouTube

Calcular los parámetros para que una funcion sea continua. Parte 2. Matematica 2 bachillerato

Continuidad de funciones
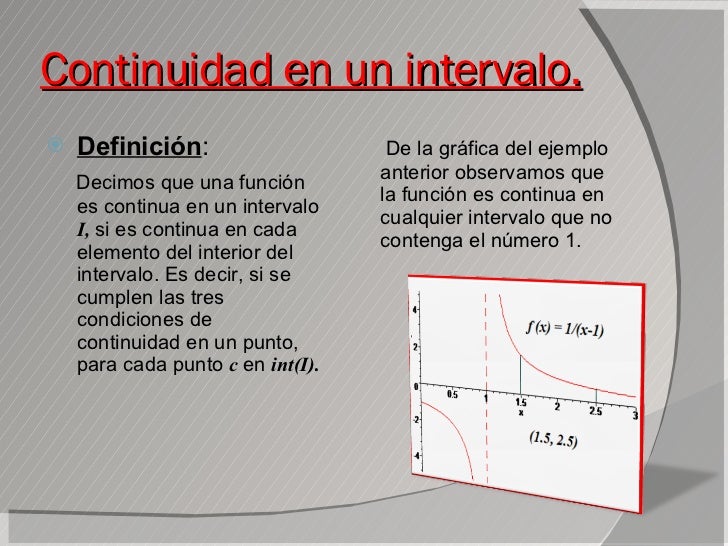
Funciones Continuas
Funció continua

Teorema Fuerte Las Funciones Continuas Son Acotadas En Compactos YouTube
Funció continua
Problema 8.98. Demostrar que cada una de las siguientes funciones reales es continua utilizando la Definición 8.96. Figura 8.5: Representación visual de la continuidad de f en a. [Math Processing Error] \boldsymbol f: R → R definido vía [Math Processing Error] \boldsymbol f ( x) = x. [Math Processing Error] \boldsymbol g: R → R definido.. Una función f es continua en el punto x=a si el límite de la función por ambos lados de a coincide con su imagen, f (a). Es decir, f es continua en x=a si. Si esto no ocurre, o bien, no existe f (a), se dice que f es discontinua en el punto x=a. Una función es continua si es continua en todos los puntos de su dominio. Ejemplo.