A sphere is defined as the set of all points in three-dimensional Euclidean space R^3 that are located at a distance r (the “radius”) from a given point (the “center”). Twice the radius is called the diameter, and pairs of points on the sphere on opposite sides of a diameter are called antipodes. Unfortunately, geometers and topologists adopt incompatible conventions for the meaning of “n.. square units. Equation of a Sphere Example. Example: Write the equation of the sphere in the standard form where the centre and radius of the sphere are given as (11, 8, -5) and 5 cm respectively.]
Ex 11.2, 6 Find radius of a sphere whose surface area Ex 11.2
Finding the Radius Formula & Concept Video & Lesson Transcript
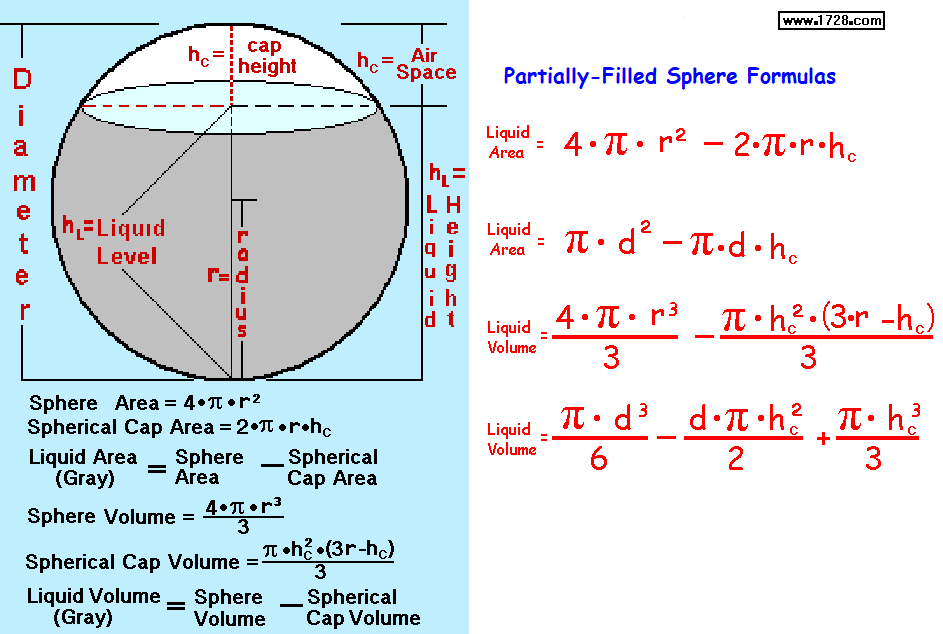
CIRCLE FORMULAS CIRCUMFERENCE, AREA ** SPHERE FORMULAS AREA, VOLUME ** CYLINDER FORMULAS
Sphere Volume Formula Math Animation YouTube
Volume of Sphere with Radius YouTube
5 Ways to Calculate the Radius of a Circle wikiHow
Equation of a circle calculator
/surface-area-1-589dd97c3df78c47588a9b3a.jpg "Math Formulas for Basic Shapes and 3D Figures")
Math Formulas for Basic Shapes and 3D Figures
Question 12 If radius of a sphere is 9 cm with error 0.03 cm
Surface Area of a Sphere Area of Sphere, Formula, Examples
Diameter of a Sphere Formula Using Volume Formula, Examples, Definition
Finding Radius of a Sphere When Given Volume YouTube
Area of Circle Definition, Formula & Examples ChiliMath
The Best Way to Find the Radius of a Sphere Wiki How To English
The Best Way to Find the Radius of a Sphere wikiHow
Question Video Finding the Equation of a Sphere given the Coordinates of Its Centre Nagwa
How to find Radius and centre of the sphere Analytic Geometry problem YouTube
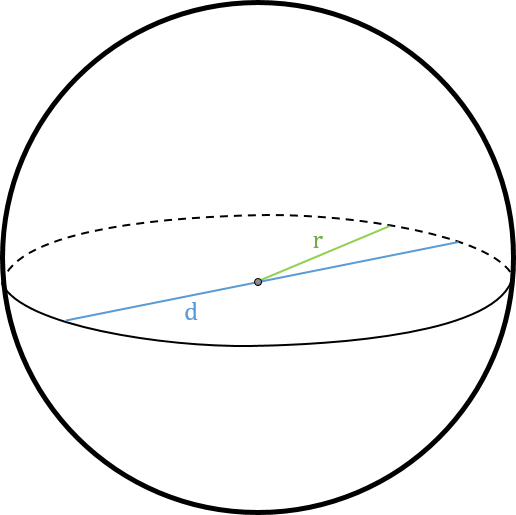
Radius of a Sphere Calculator
Equation of Sphere YouTube
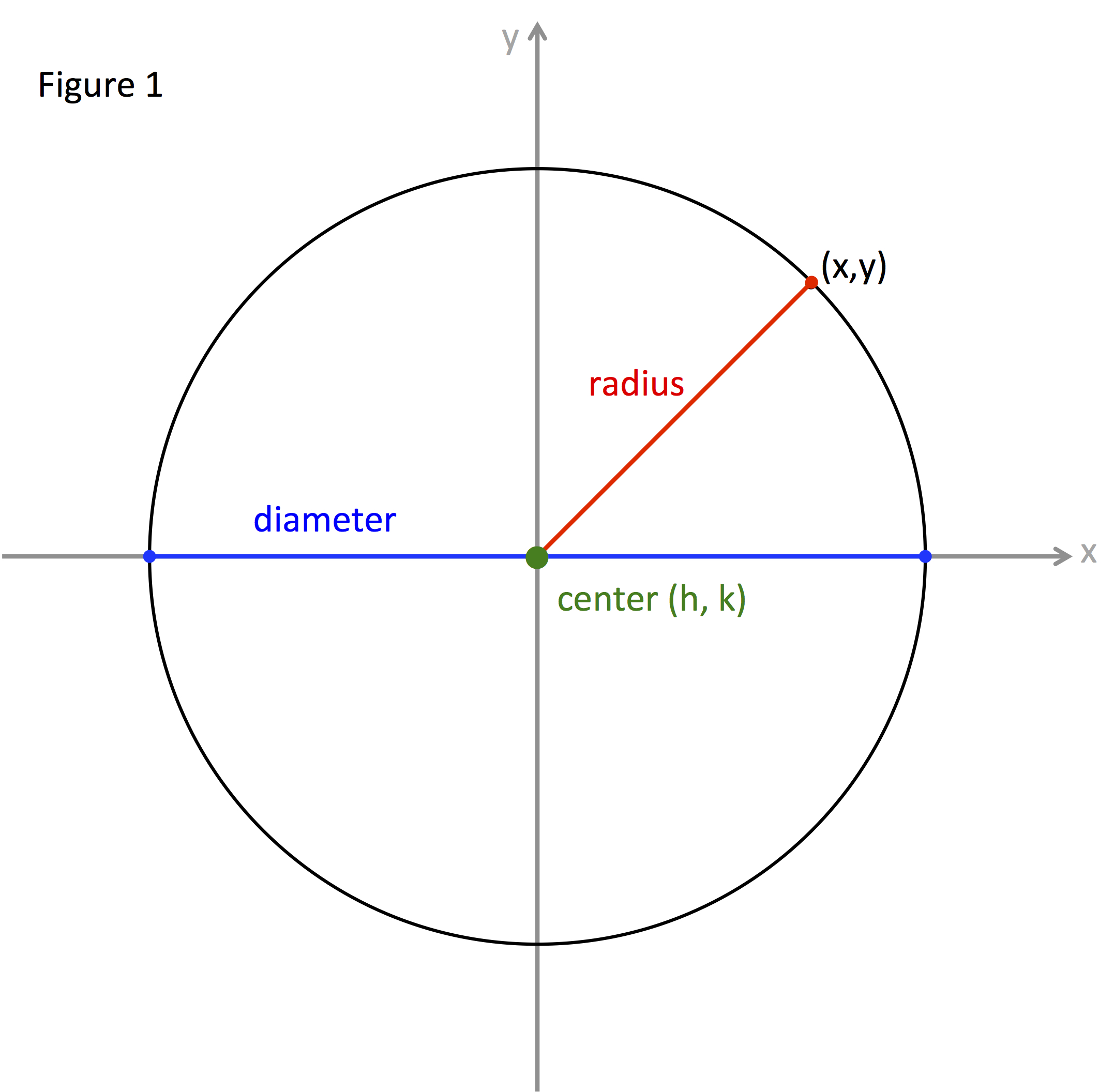
Circle CenterRadius Equation
How to find the center and radius from the equation of the sphere. Example. Find the center and radius of the sphere.???x^2+2x+y^2-2y+z^2-6z=14??? We know we eventually need to change the equation into the standard form of the equation of a sphere,. 4. Find the radius from the surface area. Use the formula r = √ (A/ (4π)). The surface area of a sphere is derived from the equation A = 4πr 2. Solving for the r variable yields √ (A/ (4π)) = r, meaning that the radius of a sphere is equal to the square root of the surface area divided by 4π.
