Na geometria, um círculo é o conjunto dos pontos internos de uma circunferência.Por vezes, também se chama círculo o conjunto de pontos cuja distância ao centro é menor ou igual a um dado valor (ao qual chamamos raio ).A área de um círculo pode ser expressa matematicamente por: = onde é o raio da circunferência e () uma constante. [1] [2]O círculo é conhecido desde antes do.. Neste artigo, você vai aprender sobre o raio, o diâmetro e a circunferência de um círculo, e como relacioná-los com a fórmula da área. Você também vai ver exemplos e exercícios para praticar seus conhecimentos. A Khan Academy é uma plataforma de ensino online gratuita e de qualidade.
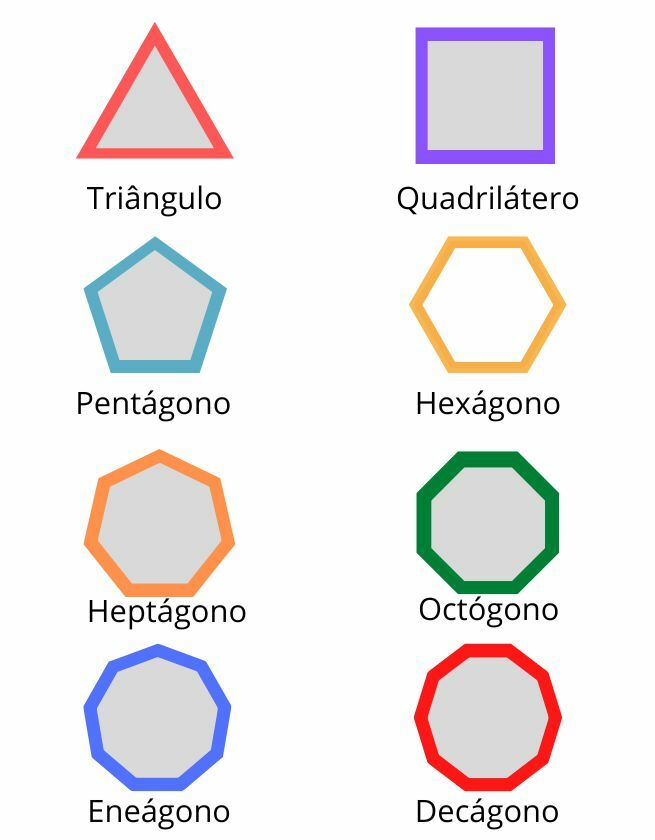
Formas Geométricas Toda Matéria

Perimetro Do Circulo O Que E Formula Como Calcular Exemplos Images

Aula 06 Classificação dos Polígonos Quanto ao Número de Lados YouTube
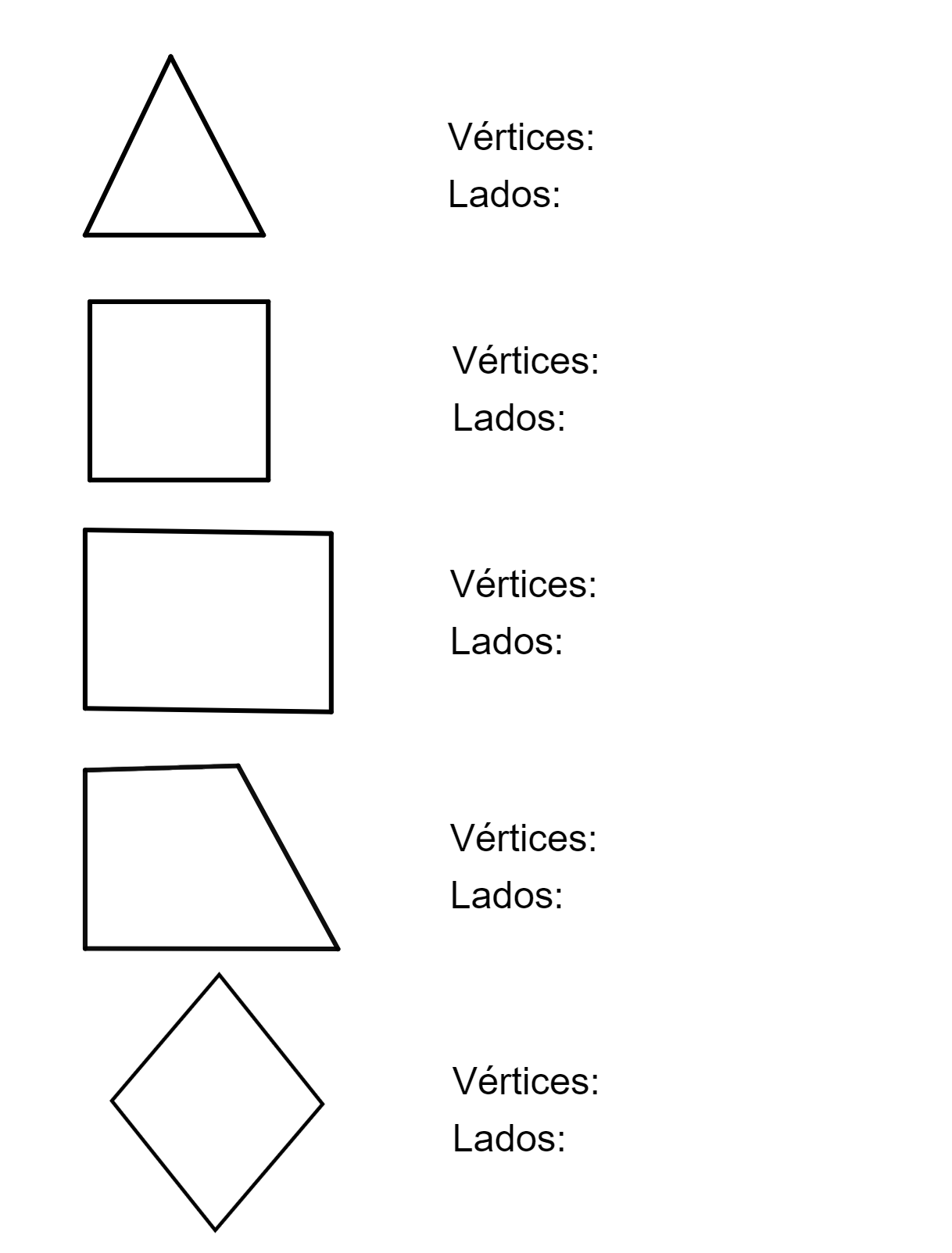
Exercícios sobre formas geométricas para o 3º ano Ensino Fundamental

Quantos Lados Tem O Círculo

DIFERENÇA ENTRE O CÍRCULO E A CIRCUNFERÊNCIA. YouTube

Matemáticas AF Circunferencia Trigonométrica

Repasamos las figuras geométricas ¿Cuántos lados tienen? Orientacion Andujar

Quantos eixos de simetria tem um círculo?

Educatoc Classificação dos Polígonos quanto ao números de lados
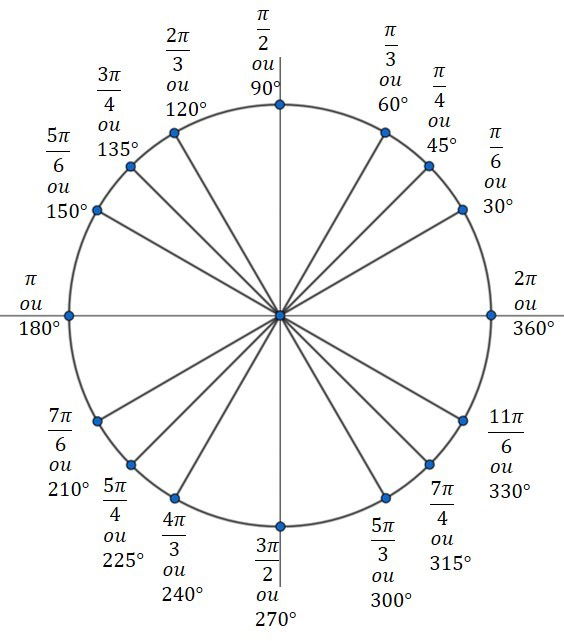
FUNÇÕES TRIGONOMÉTRICAS.

Diferença entre círculo e circunferência Quantos círculos tem na imagem? Matemática Genial
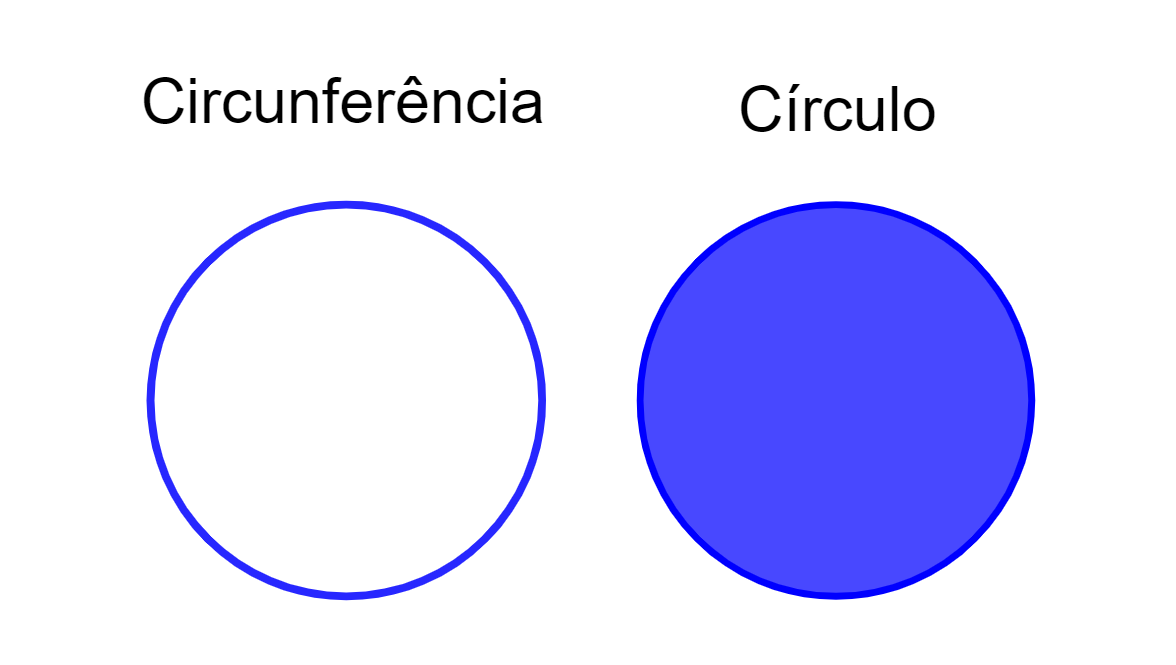
Área do Círculo O que é, fórmula, perímetro, circunferência, exemplos

O que é círculo? Brasil Escola
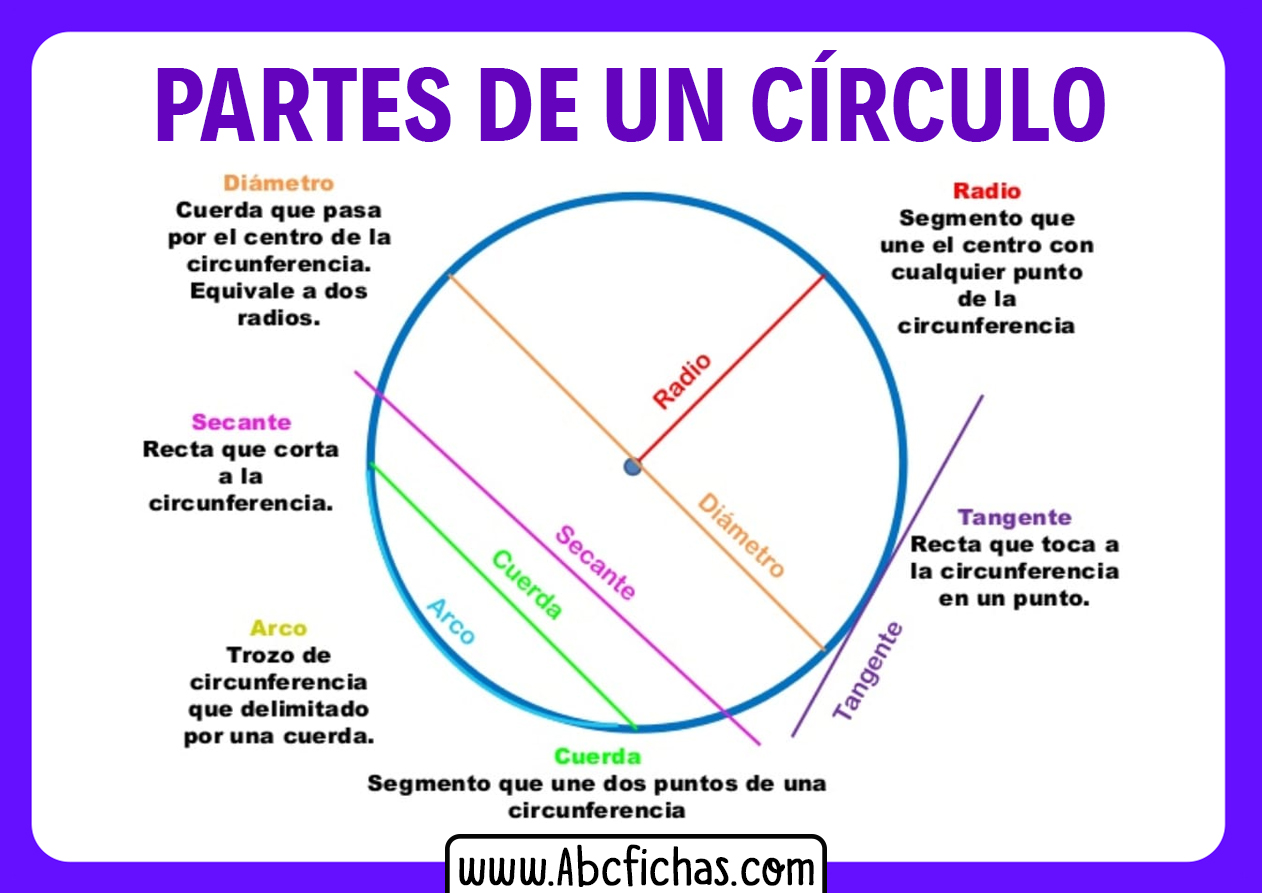
Estructura y Partes del Círculo y de la Circunferencia
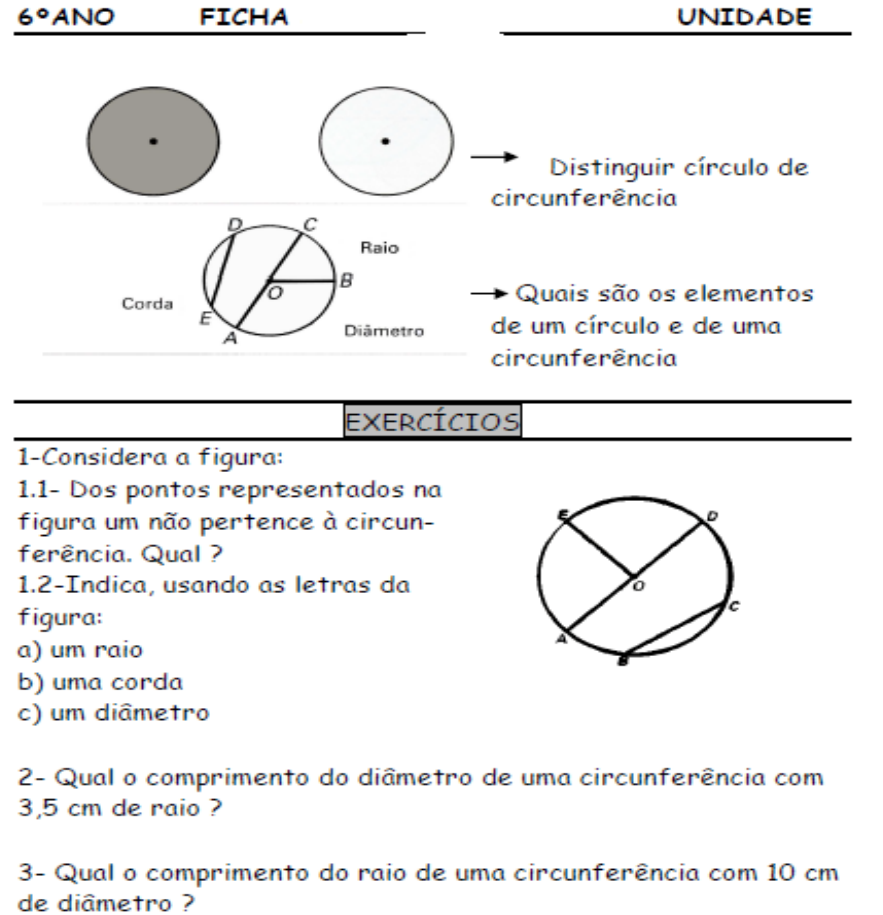
circulo e circunferência Geometria

Quantos Lados Tem O Círculo ENSINO

Polígonos e Circunferência Capítulo 4 Exercício de Aprendizagem nº 05 YouTube

Quantos Lados Tem O Círculo
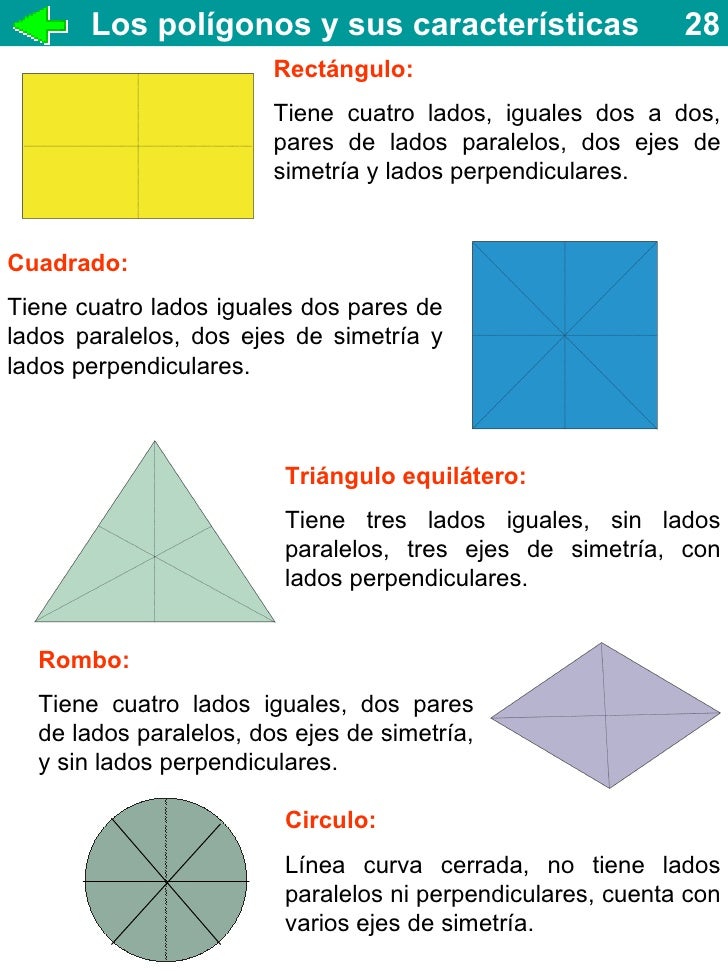
38+ Cuantos Lados Tiene El Circulo Image Lena
Um círculo é uma figura geométrica bem conhecida, mas quantos lados tem um círculo? Essa é uma pergunta comum e a resposta é simples: um círculo não tem lados. Na verdade, um círculo é definido como o conjunto de pontos que estão a uma distância igual do centro. É uma forma plana e fechada que… Continue a ler »Quantos Lados Tem Um Círculo? A Resposta Definitiva. 1º Exemplo – Calcule a área e o perímetro de um círculo cujo raio mede 25 centímetros. Solução: Como o raio mede 25 cm, basta substituir esse valor na fórmula da área e do comprimento (que é o perímetro do círculo). Para esses cálculos, lembre-se de que π é, aproximadamente, igual a 3,14: A = π·r 2. A = 3,14·25 2. A = 3,14·625.